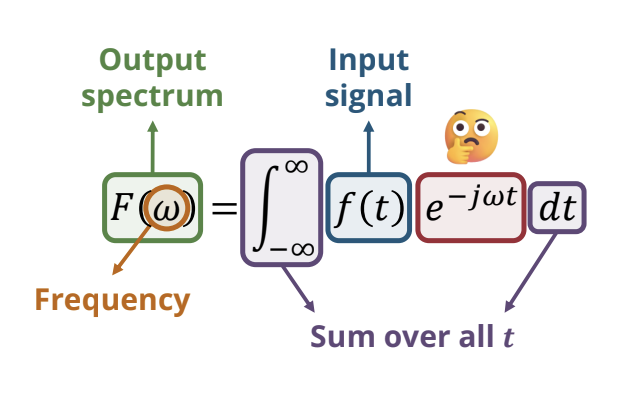
For context, see slides for Shazam Clone Week 2: Fourier Transforms and Spectrograms

STFT: Why use a window function? What's spectral leakage?

Key idea: The Fourier transform (DFT, FFT) implicitly assumes periodicity of the input signal, i.e. the signal repeats every $N$ samples.

Recall when we split $e^{-j2\pi kn/N}$ into $\mathrm{cos}(-2\pi kn/N)$ and $j\mathrm{sin}(-2\pi nk/N)$. Note that the sine and cosine repeat when $n$ increases by $N/k$ samples, so the period is $N/k$, the frequency in Hz is $k/N$, and the angular frequency in radians per sample is $2\pi(k/N)$.

This means that $e^{-j2\pi kn/N}$ completes $k$ cycles in the interval of $N$ samples (period is $N/k$).

We have the property that:

$$e^{-j2\pi k(n+N)/N} = e^{-j2\pi k(n)/N} \cdot e^{-j2\pi k} = e^{-j2\pi k(n)/N}$$

Therefore the transform itself is considered as being "periodic with period $N$ in $n$", meaning we have $f(n+N) = f(n)$. Our $e^{(\dots)}$ repeats every $N$ samples, and the DFT/FFT operates under the assumption that $x$ also repeats every $N$ samples.

Key idea, restated: The DFT/FFT interprets the input signal $x$ as a infinite-length periodic signal with period $N$.

The assumption of repetition from the (related) Fourier series process, called the periodic extension, captures this idea:

$$\tilde x[n] = x[n \textrm{ mod } N],\, n\in[0,\infty)$$

Based on this definition of repeating (the interval) $x$ over and over, we can see that when the end points of the waveform sample are not equal or have different slopes (the input signal is not periodic), we get discontinuities when we repeat the input signal:

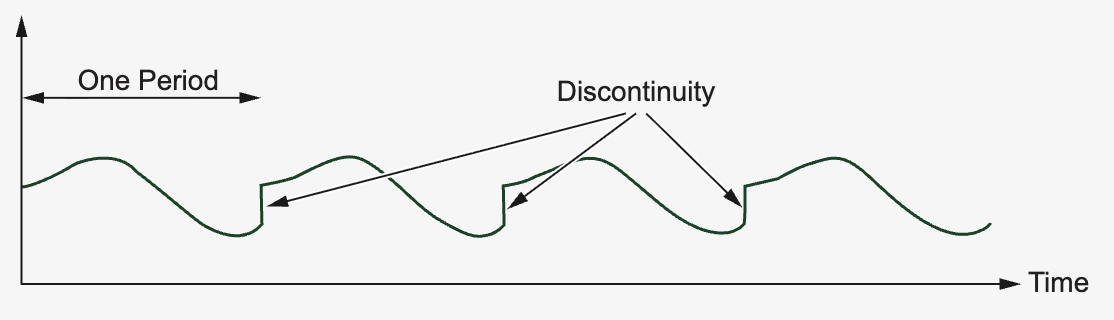
This turns an imperfect sample of a periodic wave into something that is interpreted as being much more complicated. The DFT/FFT represents this jump using other frequency bins besides the bin that corresponds to the frequency of interest. Therefore, the energy from the true frequency "spills" into many bins. This idea is spectral leakage; many frequencies are required to represent discontinuities.

You may have seen before Fourier series animations, where an SVG image storing continuous paths can be converted to a sequence of discrete points, and then reconstructed/drawn using many spinning vectors ("epicycles") found using the FFT. The more complex and winding the image, the more epicycles (sinusoids with different frequencies) are needed to reconstruct it. Spectral leakage is the same sort of idea, replacing "winding" with "containing a discontinuity".

Window functions solve this issue: by gradually reducing the amplitude of the signal to zero at the endpoints, there is less of a sharp jump to represent which concentrates the result more closely to the true frequency.

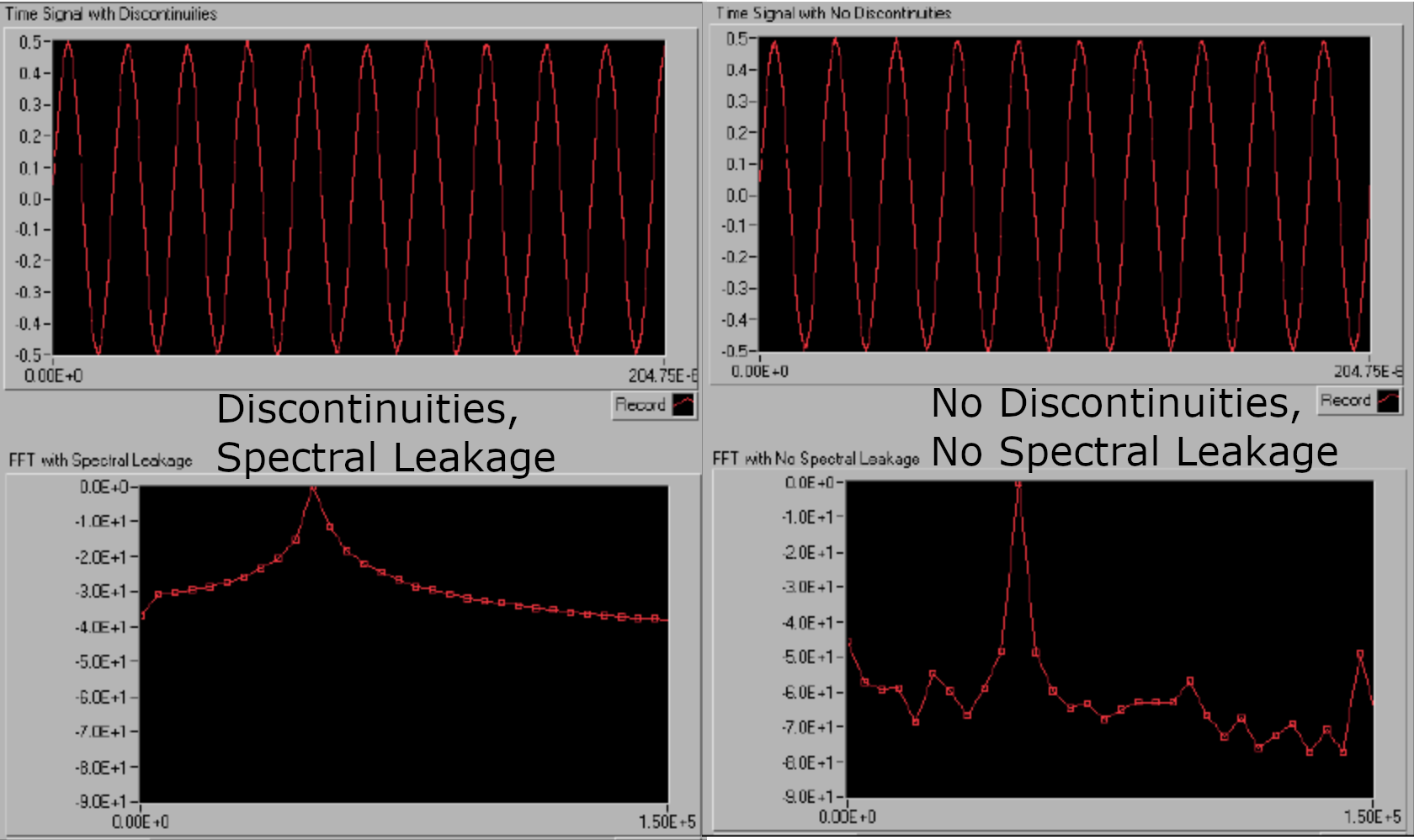
image source: (https://www.ni.com/docs/en-US/bundle/ni-scope/page/spectral-leakage.html)